Найдите точку минимума функции y=(x^2−9x+9)∙e^(x+27)

Чтобы найти наименьшее значение функции , необходимо представлять, какая у нее форма, и сделать это можно с помощью производной, ведь производная отражает динамику функции, а в случае, если производная равна 0,  это точка экстремума функции (мин или макс).
Точка минимума - это абсцисса точки, в которой функция достигает минимума.

Итак, найдем производную.
`y=(x^2−9x+9)*e^(x+27)`
`y´=(x^2−9x+9)´*e^(x+27)+(x^2−9x+9)*(e^(x+27))’`
`y´=(2x-9)*e^(x+27)+(x^2−9x+9)*e^(x+27)`
`y´=e^(x+27)(2x−9+x^2-9x+9)`

Теперь найдем значение при y´=0
`e^(x+27)(2x−9+x^2-9x+9)=0`
`e^(x+27)(2x+x^2-9x)=0`

по множителям 
`e^(x+27)=0` (не имеет решения)
`x^2+2x-9x=0` 
`x^2-7x=0`
`x(x-7)=0`
для второго множителя будут корни и они же точки экстремума
`x_1=0`
`x_2=7`

Теперь найдем значение производной, чтобы понять что происходит с функцией.

`y´(-27)=e^(x+27)(x(x-7))=1*(-27*-20)` будет больше 0
`y´(1)=e^(x+27)(x(x-7))≈3,3*-6` будет меньше 0
`y´(8)=e^(x+27)(x(x-7))` первый множитель положительный, второй тоже, значит больше 0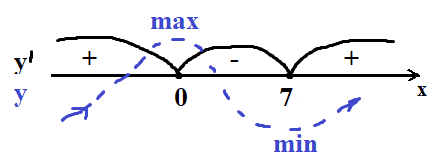

Получается, до 0 функция росла, потом убывала, потом с 7 росла. Тогда точка мин x= 7

Ответ: 7