Найдите точку максимума функции y=(x+5)^2∙e^(2−x)

Чтобы найти наибольшее значение функции , необходимо представлять, какая у нее форма, и сделать это можно с помощью производной, ведь производная отражает динамику функции, а в случае, если производная равна 0,  это точка экстремума функции (мин или макс).
Точка максимума - это абсцисса точки, в которой функция достигает максимума.

Итак, найдем производную.
`y=(x+5)^2*e^(2−x)`
`y´=(x^2+10x+25)´*e^(2−x)+(x^2+10x+25)*(e^(2−x))´`
`y´=(2x+10)*e^(2−x)+(x^2+10x+25)*e^(2−x)*(2−x)´`
`y´=(2x+10)*e^(2−x)-(x^2+10x+25)*e^(2−x)`
`y´=e^(2−x)(2x+10-(x^2+10x+25))`

Теперь найдем значение при y´=0

`e^(2−x)(2x+10-(x^2+10x+25))=0`

по множителям 
`e^(2−x)=0` (не имеет решения)

для второго множителя будут корни и они же точки экстремума
`2x+10-(x^2+10x+25)=0`
`-x^2-8x-15=0` |:-1
`x^2+8x+15=0`
`D=64-4*1*15=4=2^2`
`x_1=(-8+2)/2=-3`
`x_2=(-8-2)/2=-5`

Собственно нашли точки экстремума функции, осталось определить где функция росла, где убывала, на основании знака производной.

`y´(-10)=e^(2−x)(2x+10-(x^2+10x+25))=e^(2−x)*(2*(-10)+10-(100-100+25))=e^(2−x)*(-20-25+10)=`  значение будет отрицательное

`y´(-4)=e^(2−x)(2x+10-(x^2+10x+25))=e^(2−x)*(2*(-4)+10-(16-40+25))=e^(2−x)*(-8+10-1)=` значение будет положительное

`y´(0)=e^(2−x)(2x+10-(x^2+10x+25))=e^(2−x)*(0+10-(0+0+25))=` значение будет отрицательное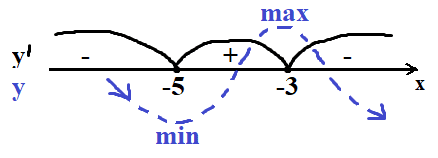

В итоге имеем, до x=-5 функция убывала, так как производная отрицательная, потом с -5 до -3 росла, после снова убывала. Значит локальная точка максимума x=-3

Ответ: -3