Найдите точку минимума функции y=1,5x^2−30x+48∙lnx+4

Чтобы найти наименьшее значение функции , необходимо представлять, какая у нее форма, и сделать это можно с помощью производной, ведь производная отражает динамику функции, а в случае, если производная равна 0,  это точка экстремума функции (мин или макс).
Точка минимума - это абсцисса точки, в которой функция достигает минимума.

Итак, найдем производную.
`y=1,5x^2−30x+48*lnx+4`
`y´=1,5*2x−30+48*1/x`
`y´=3x−30+48/x`

Теперь найдем значение при y´=0
`0=3x−30+48/x`|:3
`x−10+16/x=0` 
`x(10-x)=1*16`
`-x^2+10x-16=0`
`x^2-10x+16=0`
`D=100-4*16=36`

`x_1=(10+6)/2=8`
`x_1=(10-6)/2=2`

Теперь узнаем в пределах до и после точек экстремума, что было с динамикой функции, вычислив знаки производной для этих точек.

`y´(1)=3x−30+48/x = 3-30+48 = 21` положительная динамика
`y´(6)=3x−30+48/x= 18-30+8` отрицательная динамика
`y´(10)=3x−30+48/x = 30-30+4.8`положительная динамика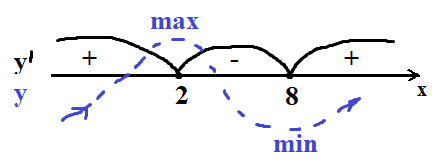

Получился слева направо по оси x у нас рост функции до 2, потом падение до 8, потом снова рост. В итоге локальный минимум значит в точке 8

Ответ: 8