8. Впишите правильный ответ.
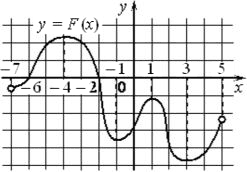
На рисунке изображён график y=F(x) одной из первообразных некоторой функции f(x), определённой на интервале (−7;5). Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [−5;2].
3
Ответ
Если взять производную от первообразной, то получится обычная функция. По сути, первообразная - это противоположность производной.
Если посмотреть на график обычной функции, тут первообразную F(x) можно считать за обычную функцию, а обычную функцию f(x) за производную. Все закономерности те же самые, что для графика обычной функции.
Для функции те участки, где есть возрастание, будут положительные, а где убывание, будут отрицательные.
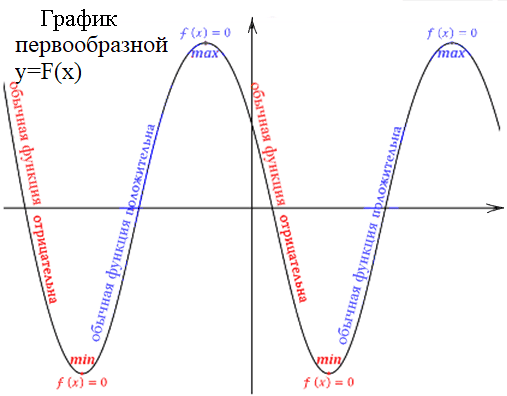
То есть у нашей функции будет 0 тогда, когда у первообразной были экстремумы, тогда был переход у функции с плюса в минус или наоборот.
У первообразной 4 экстремума, значит 4 точки (-4, -1, 1, 3) пересечения оси х.
С учетом отрезка [−5;2] остается три точки.
Ответ: 3
![]() Номер: 1E2DFC
Номер: 1E2DFC