8. Впишите правильный ответ.
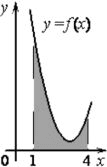
На рисунке изображён график некоторой функции y=f(x). Функция `F(x)=1/2x^3−9/2x^2+14x−10`− одна из первообразных функции f(x). Найдите площадь закрашенной фигуры.
6
Ответ
Площадь фигуры будет равна разности значений функции в ее крайних точках 1 и 4 по оси х. Используем формулу Ньютона-Лейбница.
`S = F(4)-F(1)`
`F(x)=1/2x^3−9/2x^2+14x−10`
`F(4)=1/2*4^3−9/2*4^2+14*4−10=1/2*64−9/2*16+14*4−10`
`F(1)=1/2*1−9/2*1+14*1−10`
`F(4)-F(1)=1/2*64−9/2*16+14*4−10-1/2*1−9/2*1+14*1−10=31,5-67,5+42=6`
Ответ: 6
![]() Номер: ЕГЭ 2013
Номер: ЕГЭ 2013