 Впишите правильный ответ.
Впишите правильный ответ.
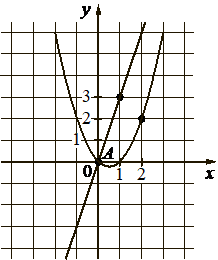
На рисунке изображены графики функций видов `f (x) = ax^2 + bx + c` и `g(x) = kx`, пересекающиеся в точках A и В. Найдите абсциссу точки В.
4
Ответ
f(x) = ax2 + bx + c
Коэффициент с равен координате у точки пересечения с осью у, т.е. с = 0.
Подставим координаты точек, принадлежащих параболе, в функцию (f(x) = ax2 + bx + c):
(–1; 2) – в 1-е уравнение значения точки параболы (–1; 2),
(2; 2) – во 2-е уравнение значение точки параболы (2; 2),
и с = 0 в оба уравнения, получим систему из двух уравнений для параболы:
`{(2 = a*(-1)^2 + b*(-1) + 0),(2 = a*2^2 + b * 2 + 0):}`
`{(2 = a – b),(2 = 4a + 2b):}`
поделим на 2 обе части второго уравнения
`{(2 = a – b),(1 = 2a + b):}`
Cложим уравнения:
`2 + 1 = а + 2а – b + b`
`3 = 3a`
`a = 3/3 = 1`
Подставим а = 1 во первое уравнение системы, найдём b:
`2 = 1 – b`
`2 – 1 = –b`
`1 = –b`
`b = –1`
Функция параболы имеет вид:
f(x) = 1* x2 – 1* x + 0 = x2 – x
Подставим точку (1; 3), принадлежащую прямой в функцию g(x) = kx и найдём k:
3 = k·1
k = 3
Функция прямой имеет вид:
g(x) = 3x
Найдём координаты абсцисс точек пересечения функций:
f(x) = g(x)
x2 – x = 3x
x2 – x – 3x = 0
x2 – 4x = 0
x(x – 4) = 0
х1 = 0 (абсцисса точки А на графике)
или
х – 4 = 0
х2 = 4 (искомая абсцисса точки В)
Ответ: 4
![]() Номер: 3D9010
Номер: 3D9010