 Впишите правильный ответ.
Впишите правильный ответ.
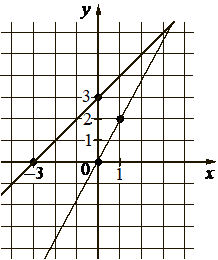
На рисунке изображены графики двух линейных функций, пересекающиеся в точке A, Найдите абсциссу точки А.
3
Ответ
На рисунке изображены прямые, линейных функции имеют вид:
y = kx + b
Найдём k и b первой функции.
На рисунке изображены графики двух линейных функций, пересекающиеся в точке A
k – тангенс угла (α) наклона прямой, по отношению к оси х. Тангенс – это отношение противолежащего катета к прилежащему катету. Найдём k:
`k = tg α = 2/2 = 1`
b – сдвиг прямой по оси у, по графику видим, прямая сдвинута от 0 на 3.
`b = 3`
Первая функция имеет вид:
`y = 1*x + 3 = x + 3`
Найдём k и b второй функции.
На рисунке изображены графики двух линейных функций, пересекающиеся в точке A.
`k = tg α = 2/1 = 2`
Прямая проходит через начало координат (0; 0), значит b = 0.
Вторая функция имеет вид:
`y = 2x + 0 = 2x`
В точке пересечения прямых значения функций (y) равны, найдём абсциссу (х) точки пересечения, то есть просто приравняем полученные ранее функции:
`x + 3 = 2x`
`3 = 2x – x`
`3 = x`
Ответ: 3
![]() Номер: 7D21DC
Номер: 7D21DC