 Впишите правильный ответ.
Впишите правильный ответ.
На рисунке изображены графики функций видов `f(x) = k/x` и `g(x) = ax + b`, пересекающиеся в точках А и B. Найдите абсциссу точки В.
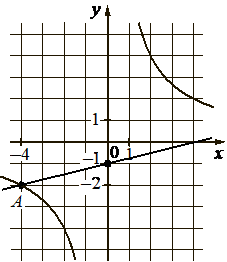
8
Ответ
`f(x) = k/x`
Подставим координаты точки (–4; –2), найдём k гиперболы:
`–2 = k/(–4)`
`k = –2·(–4) = 8`
Гипербола имеет вид:
`f(x) = 8/x`
Найдём a и b прямой g(x) = ax + b.
a – тангенс угла наклона прямой по отношению к оси х. Тангенс - это отношение противолежащего катета к прилежащему катету:
`a = tg a =1/4 = 0,25`
b – сдвиг прямой по оси у, по графику видим, прямая сдвинута от 0 на –1.
`b = –1`
Функции прямой имеет вид:
`g(x) = 0,25x – 1`
Найдём абсциссы точек пересечения функций:
`f(x) = g(x)`
`8 = (0,25x – 1) * x`
`8 = 0,25x^2 – x`
`0,25x^2 – x – 8 = 0`
`D = (–1)^2 – 4*0,25*(–8) = 9 = 3^2`
`x_(1)=(1+3)/(2*0.25)=8`
`x_(2)=(1-3)/(2*0.25)=-2/0.5=-4`
У точки А координата х = –4, значит у точки В координата х = 8.
Ответ: 8
![]() Номер: CA314B
Номер: CA314B