 Впишите правильный ответ.
Впишите правильный ответ.
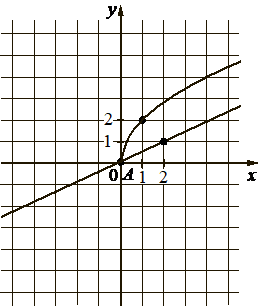
На рисунке изображены графики функций видов `f(x) = аsqrtx` и `g(x) = kx`, пересекающиеся в точках А и В. Найдите абсциссу точки В.
16
Ответ
f(x) кривой проходит через точку (1; 2), подставим значения х и у (это f(x)) в функцию, найдём а:
`f(x) = asqrtx`
`2 = asqrt1`
`2 = a·1`
`а = 2`
Значит функция имеет вид: f(x) = 2*√x
g(x) проходит через точку (2; 1), подставим значения х и у (это f(x)) в функцию, найдём k:
`g(x) = kx`
`1 = k·2`
`k=1/2=0,5`
Значит функция имеет вид: g(x) = 0,5x
Найдём абсциссу (х) точки пересечения В из системы уравнений:
`f(x)=2sqrt(x)`
`g(x)=0,5x`
`y=2sqrt(x)`
`y=0,5x`
Приравняем через y уравнения:
`2sqrtx = 0,5x`
Возведём обе части в квадрат:
`(2sqrtx)^2 = (0,5x)^2`
`4x = 0,25x^2 `
`16x = x^2`
`16x – x^2 = 0`
`x*(16 – x) = 0`
`x_1 = 0` (абсцисса точки А)
или
`16 – x = 0`
`х_2 = 16` (абсцисса точки В)
Ответ: 16
![]() Номер: 448E90
Номер: 448E90