 Впишите правильный ответ.
Впишите правильный ответ.
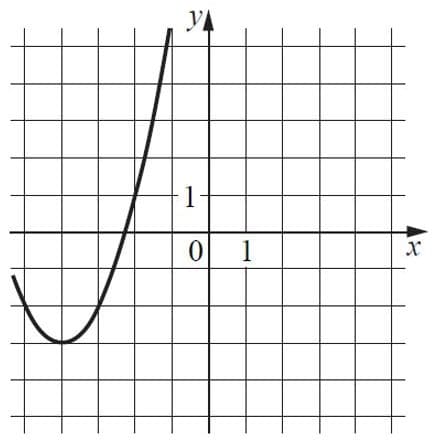
На рисунке изображён график функции `f(x)=ax^2 + bx + с`, где числа а, b и с — целые. Найдите f(−12).
61
Ответ
Ветви параболы направленны вверх, коэффициент а положительный. По вершине и ещё одной точке заметим, что при возрастании координаты х на 2, координата у вырастает на 4, т.к. зависимость квадратичная, а = 1, так как `2^2=4`
Теперь найдем вершину параболы.
Координата х вершины параболы находится по формуле:
`x=(-b)/(2a)`
х=-4,
`-4=(-b)/(2*1)`
`-b=-8`
`b=8`
В итоге получаем функцию:
`y=1*x^2+8x+c`
Если взять значения из точки (-2;1) и подставить в нее, то можно как раз узнать с
`y=1*x^2+8x+c`
`1=1*(-2)^2+8*-2+c`
`1=4-16+c`
`с=13`
получаем функцию:
`y=1*x^2+8x+13`
Теперь осталось подставить -12 вместо x, то есть x = -12 и произвести вычисления.
f(12)=144-96+13=61
Ответ: 61
![]() Номер: Демоверсия 2022
Номер: Демоверсия 2022