8. Впишите правильный ответ.
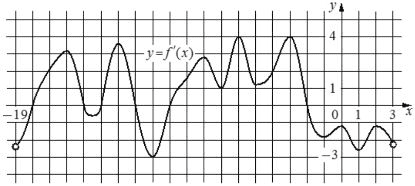
На рисунке изображён график y=f´(x) — производной функции f(x), определенной на интервале (−19;3). Найдите количество точек экстремума функции f(x), принадлежащих отрезку [−17;−4].
4
Ответ
Так как производная является отражением динамики функции, то пиковые значения этой самой функции, то есть минимум и максимум, где идет изменение тенденции с роста на падение или наоборот, станут теми самыми точками, когда динамика на этом пике будет равна нулю, а производная получится положительная - 0 - отрицательная или отрицательная - 0 - положительная, то есть будет иметь пересечение с осью x, а значит образуются корни. Корни производной являются точками экстремума для самой функции.
Делаем вывод, точки экстремума функции будут там, где производная равна 0, то есть где график пересекает ось х.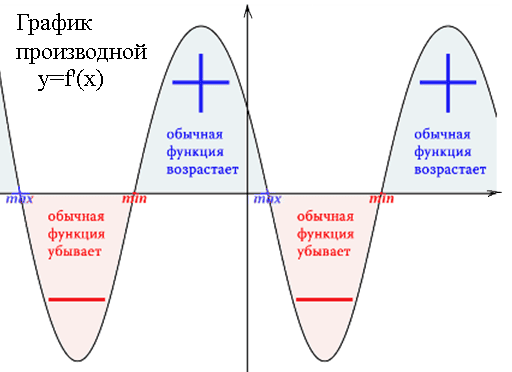
| Области | [− 17; − 15) | -15 | (-15;-14) | -14 | (-14;12) | -12 | (-12;-10) | -10 | (-10; -4) |
| Значение производной (динамика функции) |
+ | 0 | - | 0 | + | 0 | - | 0 | + |
| Что с функцией? | растет↑ | макс | убывает↓ | мин | растет↑ | макс | убывает↓ | мин | растет↑ |
На отрезке [−17;−4] 4 точки, где производная равна 0 и меняет свой знак.
Ответ: 4
![]() Номер: 0ED279
Номер: 0ED279