Найдите точку максимума функции y=−x/(x^2+225)

чтобы найти наибольшее значение функции , необходимо представлять, какая у нее форма, и сделать это можно с помощью производной, ведь производная отражает динамику функции, а в случае, если производная равна 0,  это точка экстремума функции (мин или макс).
Точка максимума - это абсцисса точки, в которой функция достигает максимума.

Итак, найдем производную.
`y=−x/(x^2+225)`
`y´=((−x)´(x^2+225)-(-x)(x^2+225)´)/(x^2+225)^2`
`y´=(-1(x^2+225)+x*2x)/(x^2+225)^2`

Теперь найдем значение при y´=0

`(-x^2-225+2x^2)/(x^2+225)^2=0`
`(x^2-225)/(x^2+225)^2=0`

по знаменателю
`x^2+225≠0` (нет x удовлетворяющего условию)

по числителю
`x^2-225=0`
`x_1=15`
`x_2=-15`

Нашли точки экстремума, теперь найдем, где максимум и где минимум. Возьмем, скажем, -20, 0, 20. Находим только знаки для числителя, знаменателя и в итоге для значения

`y´(-20)=((-20)^2-225)/((-20)^2+225)^2=+/+...` это будет значение со знаком плюс
`y´(0)=(0^2-225)/(0^2+225)^2=-/+` это будет значение со знаком минус
`y´(20)=(20^2-225)/(20^2+225)^2=...` это будет значение со знаком плюс.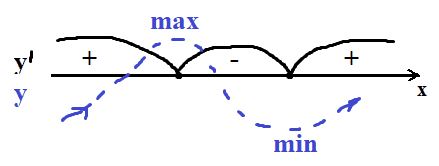

Получается у нас до -15 функция росла, потом с -15 до 15 убывала, потом с 15 до бесконечности росла. Значит локальный максимум получился в точке x=-15

Ответ: -15