13. Впишите правильный ответ.
Найдите объём правильной четырёхугольной пирамиды, сторона основания которой равна 4, а боковое ребро равно `2sqrt11`.
32
Решение
Объем пирамиды можно найти по формуле из справочных материалов ЕГЭ:
`V=1/3*S*h`, где S - площадь основания, h - высота.
С площадью квадрата в основании проблем не будет, а высоту придется поискать. Делаем для наглядности дополнительные построения: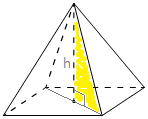
Находим диагональ основания по теореме Пифагора:
`x^2=4^2+4^2`
`x=sqrt32`
`x=4sqrt2`,
тогда половина диагонали равна `2sqrt2`.
Находим высоту (по теореме Пифагора)
`h^2=(2sqrt11)^2-(2sqrt2)^2`
`h^2=4*11-4*2`
`h^2=44-8=36`
`h=6`
Находим объем
`V=1/3*S*h=1/3*4*4*6=32`
Ответ: 32
Номер по ФИПИ: FB0748