13. Впишите правильный ответ.
Через точку, делящую высоту конуса в отношении 1 : 2, считая от вершины, проведена плоскость, параллельная основанию. Найдите объём этого конуса, если объём конуса, отсекаемого от данного конуса проведённой плоскостью, равен 10.
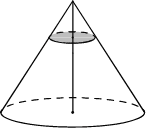
270
Решение
Объем конуса можно найти по формуле
`V=1/3*π*r^2*h` , где `π*r^2` - площадь основания, а h - высота.
Отношение радиусов будет равно отношению высот большого конуса и маленького. Тогда можно записать объем для большого конуса
`V_1=1/3*π*r^2*h`
и для маленького с учетом, что его h является частью (1:2), то есть всего 3 части и 1/3 часть приходится на высоту маленького конуса.
`V_2=1/3*π*(1/3*r)^2*1/3*h`
а отсеченная часть будет разность между объемом большого и малого конуса
`V_(отсеч)=1/3*π*r^2*h - 1/3*π*(1/3*r)^2*1/3*h=1/3*π*r^2*h (1-1/9*1/3)=1/3*π*r^2*h*26/27`
...мы видим, что это 26/27 от нашего объема большого конуса (то есть получили формулу выше с коэффициентом 26/27) и это и есть Vотсеч.
Тогда полный объем большого конуса находим так. 10 это 1 часть из 27, а 26 частей отсекается, то есть объем большого конуса будет
10*(26+1)=270
Ответ: 270
![]() Номер по ФИПИ: 31CA99 ⭐
Номер по ФИПИ: 31CA99 ⭐