13. Впишите правильный ответ.
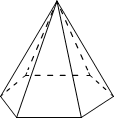
Стороны основания правильной шестиугольной пирамиды равны 12, боковые рёбра равны 10. Найдите площадь боковой поверхности этой пирамиды.
288
Решение
Так как основание - правильный шестиугольник, то все стороны пирамиды - равнобедренные треугольники.
Найдем площадь боковой стороны по формуле Герона (формулы нет в справочных материалах, ее нужно запомнить):
`S=sqrt(p(p-a)(p-b)(p-c))`
p-полупериметр, a,b,c - стороны треугольника
`p = (12+10+10)/2=32/2=16`
`S=sqrt(16(16-12)(16-10)(16-10))=sqrt(16*4*6*6)=48`
Узнаем площадь всей боковой поверхности
48*6=288
Ответ: 288
Номер по ФИПИ: 514C0F