13. Впишите правильный ответ.
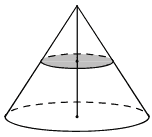
Объём конуса равен 8. Через середину высоты конуса проведена плоскость, параллельная основанию. Найдите объём конуса, отсекаемого от данного конуса проведённой плоскостью.
...
Решение
Объем конуса можно найти по формуле
`V=1/3*π*r^2*h` , где π*r2 - площадь основания, а h - высота.
Отношение радиусов будет равно отношению высот большого конуса и маленького. Тогда можно записать объем для большого конуса
`V_1=1/3*π*r^2*h`
и для маленького с учетом, что его h является частью (1:1), то есть всего 2 части и 1/2 часть приходится на высоту маленького конуса.
`V_2=1/3*π*(1/2*r)^2*1/2*h`
а отсеченная часть будет разность между объемом большого и малого конуса
`V_(отсеч)=1/3*π*r^2*h - 1/3*π*(1/2*r)^2*1/2*h=1/3*π*r^2*h (1-1/4*1/2) = 1/3*π*r^2*h*7/8`
Тогда мы видим, что это 7/8 от нашего объема конуса (то есть получили формулу выше с коэффициентом 7/8) и высчитываем Vотсеч.
`8*7/8=7` это объем отсеченного. При этом
8-7=1 это объем отсеченного маленького конуса
Ответ: 1
Номер по ФИПИ: 5A6C02 ⭐