Найдите AD, если BC=12. Задание 25 ОГЭ по математике (геометрия), ФИПИ

Поскольку существует точка, равноудалённая от всех вершин четырёхугольника, четырёхугольник можно вписать в окружность. Четырёхугольник вписан в окружность, следовательно, суммы противоположных углов равны 180°:
∠BAD + ∠BCD =180° 
∠BAD = 180° - ∠BCD
∠BAD = 180° - 95° = 85°
Отрезки AM,BM и CM равны как радиусы окружности, поэтому треугольники ABM и BMC — равнобедренные, откуда
∠BAD = ∠ABM = 85° и
∠ВCМ = ∠MBC = ∠ABC - ∠ABM = 115° - 85° = 30°
Рассмотрим треугольник BMC. Сумма углов в треугольнике равна 180°, откуда
∠BMC = 180° - ∠MBC - ∠ BCM = 180° - 30° - 30° = 120°
По теореме синусов найдём сторону BM из треугольника BMC:
`(BC)/(sinBMC)=(BM)/(sinBCM)`
`BM = ВС * (sinBCM)/(sinBMC)`
`BM=(12*sin30°)/(sin120°)=(12*1/2)/(sqrt3/2)=4sqrt3`
Сторона AD — диаметр описанной окружности, поэтому
`AD=2BM=2*4sqrt3=8sqrt3`
Ответ: 8√3

2 способ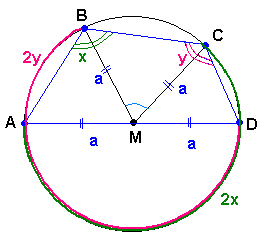

Точка М равноудалена от вершин. Поскольку существует точка, равноудалённая от всех вершин четырёхугольника, четырёхугольник можно вписать в окружность.
AD - диаметр.
дуга АС = 2 ∠В = 2 ∙ 115° = 230°
дуга ВЕ = 2 ∠С = 2 ∙ 95° = 190°
Сумма всех дуг окружности 360°
ВС + АС + BE – 180° = 360°
BC + 230° + 190° - 180° = 360°
BC + 240° = 360°
BC = 120°
∠BMC опирается на дугу ВС, ∠BMC = ВС = 120°
∆BMC равнобедренный треугольник, ВС = 12, ∠BMC = 120°
по т. косинусов
BC² = a² + a² – 2 ∙ a ∙ a ∙ cos 120°
BC² = a² + a² – 2 ∙ a ∙ a ∙ ( – 1/2)
BC² = a² + a² + a²
BC² = 3a²
a² = BC²/3
a² = 12²/3
a² = 144/3
а² = 48
а = 4√3 
АЕ = 2а = 2 ∙ 4√3  = 8√3 
Ответ: 8√3