2. Впишите правильный ответ.
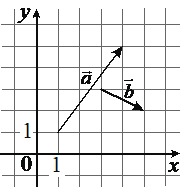
На координатной плоскости изображены векторы `veca` и `vecb`, координатами которых являются целые числа. Найдите длину вектора `veca` +4`vecb`.
11
Решение
Координаты вектора: если `A(x_1;y_1)` и `B(x_2;y_2)`, то `vecAB(x_2-x_1;y_2-y_1)`
Умножение вектора на число: если `veca(2;3)`, то `2veca(4;6)`
Сложение векторов: если `veca(x_1;y_1)` и `vecb(x_2;y_2)`, то `veca+vecb=(x_1+x_2;y_1+y_2)`
Длина вектора: если `veca(x;y)`, то `|veca|=sqrt(x^2+y^2)`
`veca(4-1;5-1)=(3;4)`
`vecb(5-3;2-3)=(2;-1)` ,
`4vecb (8;-4)`
Координаты искомого вектора будут равны сумме соответствующих координат:
`veca +4 vecb (x_1+x_2; y_1+y_2) = veca +4 vecb (3+8; 4-4) = veca +4 vecb (11; 0)`
А теперь находим его длину
`|veca +4vecb|= sqrt(11^2+0^2)=11`
Ответ: 11
![]() Номер: 579B74
Номер: 579B74