25. Дайте развернутый ответ.
В трапеции ABCD основания AD и BC равны соответственно 18 и 6, а сумма углов при основании AD равна 90°. Найдите радиус окружности, проходящей через точки A и B и касающейся прямой CD, если AB=10.
Впишите радиус
10
Решение
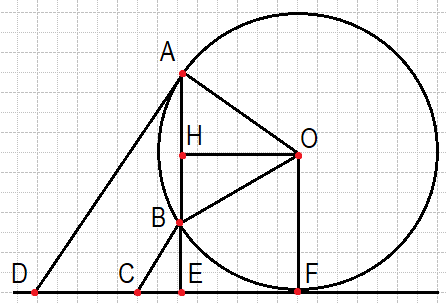
Продолжим стороны AB и CD до их пересечения в точке E. Угол AEC равен 90°, поскольку сумма углов EAD и EDA равна 90°. Рассмотрим треугольники AED и BEC, они прямоугольные, углы ECB и EDA равны как соответственные углы при параллельных прямых, следовательно, эти треугольники подобны, откуда
`(AE)/(BE)=(AB+BE)/(BE)=(AD)/(BC)`
отсюда выразим BE
`(AB+BE)/(BE)=(AD)/(BC)`
`BC*(AB+BE)=AD*BE`
`BC*AB+BC*BE=AD*BE`
`AD*BE-BC*BE=BC*AB`
`BE*(AD-BC)=BC*AB`
`BE=(BC*AB)/(AD-BC)`
Подставляем значение находим BE
`BE=(BC*AB)/(AD-BC)=(6*10)/(18-6)=60/12=5`
Пусть окружность касается прямой CD в точке F, причём точка F может лежать или на стороне CD или на её продолжении. Отрезок OF перпендикулярен прямой CD, как радиус проведённый в точку касания, OA,OB и OF — радиусы.
Треугольник AOB — равнобедренный, OH — высота, следовательно, OH является медианой и биссектрисой. Четырехугольник OHEF — прямоугольник, потому что все его углы прямые. Откуда:
`R=OF=HE=HB+BE=(AB)/2+BE=5+5=10`
Ответ: 10
![]() Номер: 4D1DBB
Номер: 4D1DBB